”Felsvaren kan vara avgörande för lärandet”

Jenny Svantesson Wester har just avslutat en lektion om division och multiplikation i årskurs 7 när hon träffar Lärare & Forskning för att berätta om hur hon använder och utvecklar uppgifter i undervisningen. Hon är påtagligt upprymd, entusiastisk och glad över lektionen och resultatet.

– Eleverna fick själva syn på hur det hänger ihop! Vi tittade närmare på division med tal mindre än 1 – som kan vara svårt att förstå intuitivt, men som kan visa vad division är. Nu nådde vi dit jag hoppats med att klura ut vad 8 delat med 0,25 blir!

Inte den enklaste vägen

Jenny beskriver en 45-minuterslektion som krävde att eleverna ansträngde sig för att komma fram till rätt svar. Hennes egen roll framstår som en väl förberedd lärare som är nyfiken på hur eleverna tänker för att kunna guida mot lösningarna.

– Eleverna fick kämpa en del, men det är avgörande att jag inte berättar hur de ska tänka eller vad det rätta svaret är förrän vi tillsammans har konstaterat vad som kan vara rätt eller fel. Jag vet att de kan själva om de bara får hjälp att hitta rätt. Och det är inte den enklaste vägen varken för mig eller eleverna.

”Värsta gissningen bättre än att inte veta hur eleven tänker”

Hur gick lektionen till?

– Det här är en klass med hög andel F i matematik. Syftet med lektionen var att öka förståelsen om divisionsräkning och multiplikation. Att dela med något som är mindre än 1 ger möjlighet för eleverna att få syn på hur division och multiplikation hänger samman så att de kan tillämpa den förståelsen i stället för att lära sig något utantill och mer mekaniskt lösa tal vilket inte nödvändigtvis innebär att man förstår.

– Vi började med uppgiften 6 delat på 0,5. Jag skrev upp talet på tavlan och lät eleverna fundera en stund. I det här skedet vill jag som lärare att stämningen ska vara sådan att eleverna vågar prata och tänka högt utan att känna att det som de säger behöver vara rätt: den värsta gissningen är bättre än att jag inte får veta alls hur eleven tänker.

– Efter ett tag fick de var och en säga vad de tror att svaret blir. Ganska många sa 3 och fler sa ”jag vet inte”. Då sa jag till en av de eleverna att ”jag tror visst att du har tankar om det här talet fast du kanske är ovan vid att säga det. Nästa gång får du vara med och svara!” Om vi tillåter eleverna att alltid säga ”jag vet inte” är det svårt att komma vidare!

”Nu vill jag att de själva ska få syn på att det här kanske inte stämmer”

– Nu har vi alltså talet 3 som svar och då får vi gå vidare och ta reda på om det stämmer. Här får jag ju inte säga ”nej” eller antyda om det är fel eller rätt eftersom jag vill att eleverna ska förstå att deras svar är viktiga och räknas för att vi ska komma vidare. Så jag fyller i 3 som svar på tavlan. Nu vill jag att de själva ska få syn på att det här kanske inte stämmer, men då behöver vi ett nytt perspektiv. Så jag tackade för svaren och gick vidare till 6 delat på 2. Då svarade alla att svaret är 3 som jag också skrev upp på tavlan så att vi hade två svar som är 3. Eleverna började fundera på om det där kunde stämma, men vi fokuserade på 6 delat på 2 eftersom de såg något där som de förstod. Vi bekräftade det tydligt tillsammans i klassrummet: har man 6 och delar det med 2 så blir ju det 3!

– När jag var säker på att alla var med på det så gick vi tillbaka till det där med att dela med en halv. Då var det fler som vågade säga något och några menade att det nog skulle vara en decimal i svaret eftersom det var en decimal i talet som vi delade med. OK! Då gick vi tillbaka till det vi alla visste: 6 delat på 2. Jag frågade om det inte finns fler sätt att se på den uträkningen? Kan man inte fråga hur många gånger 2 får plats i en 6:a? Man gör alltså innehållsdivisionen. ”Jo”, svarade eleverna och då konstaterade vi att man kan tänka på två olika sätt!

– Så långt in i lektionen ville jag befästa att man kan tänka på olika sätt och få alla att hänga med en gång till: ”vi gör likadant med 6/1”! Då kunde alla svara att om man delar en 6:a i en hög får man en 6:a och sex stycken 1:or får plats i en 6:a.

Ska själva kunna generalisera

Jenny beskriver att hon är ute efter att eleverna ska kunna generalisera utifrån sådant de vet. Om 6 delat med 2 är 3 eftersom 2 får plats 3 gånger i 6 så borde det gå att räkna ut vad 6 delat med en halv är genom att räkna ut hur många halva ettor som får plats i 6.

– OK! Då gick vi tillbaka och testade den metoden på det där första talet med 0,5: vad är egentligen 0,5? Då svarade några att det är en halv 1:a. OK! Hur många gånger får en halv 1:a plats i 6? Då sa några elever att det verkade vara ett väldigt konstigt svar, men kunde det vara 12? Ja, då fick vi kolla det och ritade upp det och visst: det funkade ju! Nu hade de löst uppgiften!

– Men i det läget är det för tidigt att luta sig tillbaka och konstatera att ”nu kan de det!”, säger Jenny som på lektionen ville befästa kunskapen genom att multiplicera och visa hur division och multiplikation hänger ihop.

– Eleverna fick då uppgiften att tillsammans räkna ut 6 x 0,5 och tyckte att det var svårt. Någon multiplicerade med femman så det blev 30, men ingen klarade av uträkningen så jag frågade om man kan göra samma sak som vi hade gjort tidigare: ”vad är 6 x 1?” och ”vad är 6 x 2?”. Det kunde de lösa, men jag ville att de skulle få syn på vad de gjorde, vad som hände, och till slut sa någon ”Aha! Om vi tar sexan bara en halv gång? Då blir det 3! Nu var alla med på att om man multiplicerar med en halv så blir det mindre och delar man så blir det ett större tal!

En ”enkel” uppgift tog 45 minuter

– Nu var eleverna mogna att gå vidare och jag introducerade 8 istället för 6 och gav uppgiften 8 delat med 0,5. Efter mycket resonerande löste de den uppgiften och då kom vi fram till det som jag hoppades att jag skulle nå under lektionen: 8/0,25. Vi resonerade och alla var med på lösningen att det blev 32. För att befästa vände jag till multiplikation och visst: 8 x 0,25 blir bara 2!

En till synes kort och enkel uppgift: ”vad är 6 delat med en halv” krävde 45 lektionsminuter.

– De tänker och de kämpar och när de inte kan får de gå tillbaka till det de kan för att klura ut vägen framåt. Men de får möjlighet att förstå multiplikation och division på ett djupare plan så att de kan tillämpa räknesätten på decimaltal och verkligen förstå.

Så många som möjligt deltar

Lektionen som Jenny Svantesson Wester just beskrivit har hon också använt på äldre elever när hon undervisat som lektor och hjälpt lärare att utveckla sin matematikundervisning.

– Jag använde den i en nia där flera elever inte trodde sig kunna förstå: matten hade flugit över huvudet på dem, men med den här lektionen fick jag med mig även dem! När de själva räknat ut vad 8 x 0,25 är så bara strålade det om dem! De hade tidigare inte fått hänga med på första steget och tappat intresset och tron på att de skulle förstå. Tack vare att de fick chansen att ta de första stegen så hängde de med hela lektionen.

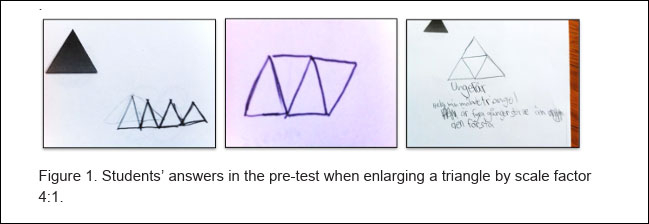
Skisserna är hämtade från ett forskningsprojekt och visar hur elever på olika sätt uppfattar innebörden av att förstora en triangel i skala 4:1. Med utgångspunkt i elevernas olika uppfattningar av det matematiska innehållet kan undervisningen utformas och utvecklas för att öka eleverna delaktighet i undervisningen och också öka deras möjligheter att få en djupare förståelse för den matematik som lektionen handlar om.

Jenny Svantesson Wester betonar vikten av att så många som möjligt är med från början.

– Du kan ta en stor uppgift i huvudräkning och plocka ut en del eller se det som flera små uppgifter där du skruvar lite, lite för att befästa och gå vidare till nya uppgifter.

Ingen del i Jennys val av uppgifternas innehåll är en slump.

– Om någon frågar mig varför jag använde just 6 delat på 1 så kan jag svara på det! Jag vet vad det är eleverna ska få syn på och har valt de uppgifter som leder till det jag vill med lektionen. Man kan inte ta för givet att uppgifter i sig är bra. Det måste finnas en tanke med varje förändring: jag kanske vill få bekräftat att eleverna kan generalisera eller så vill jag visa en kontrast för att förstärka förståelsen.

”Måste ta med eleverna på resan”

Jenny förstår att eleverna ibland tycker att hon bara borde berätta ”hur man räknar ut” så att de kan göra det snabbt och enkelt.

–  Visst vore det så mycket enklare på sätt och vis, men så kan vi inte göra om eleverna ska lära sig! Vi måste ta med dem på resan och de måste hitta sin egen krokiga väg!

Jenny Svanteson Wester forskar parallellt med sitt uppdrag som lektor på högstadiet på Nytorpsskolan i Hammarkullen, Göteborg, samt med en särskild satsning på matematik i gymnasiet. Hon planerar att publicera resultaten av sin forskning vid Göteborgs universitet under de närmaste åren.