TEMA UPPGIFTER I MATEMATIK
PROFESSORN INGER ERIKSSON:
”En bra uppgift ger eleven chans att förstå något som den ännu inte kan”
Uppgifter i matematik kan utveckla en djupare förståelse, men då måste läraren veta vad eleverna behöver lära sig för att förstå, exempelvis genom att analysera felsvar, menar Inger Eriksson, professor i pedagogik vid Stockholms universitet.
– Det räcker inte att veta att de gör fel utan framför allt varför – och vad de behöver lära sig för att lösa uppgiften.
Inger Eriksson svarar snabbt och entusiastiskt under intervjun med Lärare & Forskning, men är noggrann med orden. Hon förtydligar ett av sina svar med ordet ”ännu”:
– En bra uppgift ger eleven chans att förstå något som den ännu inte kan. Det där måste man påminna sig om: att eleverna kan lära sig om de får möjlighet – frågan är bara hur undervisningen ska utformas för att bli lärande.
– Man kan få ut otroligt mycket av att försöka komma underfund med vad det är som eleverna ännu inte riktigt kan, det som de inte har urskilt och ställa det i relation till vad det är man kan – när man kan?
Utformningen avgörande
Som handledare åt forskarstuderande och som projektledare för en stor mängd studier i klassrum och tillsammans med lärare i matematik har Inger Eriksson studerat hur utformningen av uppgifter kan bli avgörande för att alla elever får chansen att introduceras till matematiken eller kunna ta stegen in i mer avancerade problemlösningar och uträkningar. Hennes slutsats är att frågans innehåll – och hur läraren agerar i klassrummet – är avgörande för hur en uppgift kan leda till lärande.
– Därmed inte sagt att undervisningen är beroende av lärarens personlighet utan det handlar om hur läraren behandlar innehållet i uppgiften. En uppgift som inte verkar speciellt avancerad kan bli väldigt berikande för eleverna beroende på hur läraren jobbar med uppgiften och eleverna.
Procedurell färdighet
De uppgifter som effektivt kan utveckla generella strategier, som eleven kan tillämpas på olika typer av problem, kan kallas öppna eller rika i betydelsen att de har flera olika lösningar, leder till resonemang och egna beslut av eleven samt gärna vara kopplade till verkliga omständigheter. Inger Eriksson har i flera forskningsprojekt om matematikundervising tillämpat forskarna Vasilii Davydov och Daniil Elkonins teorier om lärandeverksamhet som utgår från att undervisningen ska främja matematiskt tänkande, förståelsen av matematiska begrepp, relationer och varför vissa metoder fungerar snarare än hur man räknar. Procedurell färdighet, att kunna följa regler eller göra steg för steg-uträkningar, bör vara grundad i begreppsförståelse, menar hon.
– En uppgift som innebär att eleven, eller elever tillsammans, kan utforska problemet, det vill säga analysera vari problemet består och sedan pröva och argumentera för möjliga lösningar kan leda till en djupare förståelse. Det är också betydelsefullt att eleverna får uppleva att deras nuvarande modeller och strategier inte helt räcker till – att de behöver lära sig något nytt.
Fråga i stället för bekräfta
En förutsättning för att elevernas lärande ska utvecklas är att undervisningen omfattar det som behöver utvecklas och tar tag i de främsta utmaningarna för elevernas lärande. Då krävs att läraren är lyhörd för elevernas frågor och reaktioner, menar Inger Eriksson.
– Ett exempel är att vi är vana med att vara väldigt bekräftande när en elev resonerar i ett svar. Vi nickar och bekräftar att eleven är på rätt väg, fortsätt så! Men vi vet från studier att det kan hindra utvecklingen av resonemanget, prövandet och argumenterandet. Och när de andra eleverna märker att en elev har en lösning så behöver de ju inte engagera sig. Men om läraren i stället frågar ”är det någon som kan förklara det här på ett annat sätt” eller säger ”nu hängde jag inte med” så kan fler elever engageras och de måste resonera vidare och pröva andra lösningar.

”En uppgift som inte verkar speciellt avancerad kan bli väldigt berikande för eleverna beroende på hur läraren jobbar”
”Learning study”
Att det går att förbättra uppgifter för att öka elevernas förståelse för matematik visar flera forskningsstudier. En metod som används i studier om att utveckla undervisning är learning study som innebär att forskare och lärare tillsammans utvecklar uppgifterna och undervisningen gradvis. Med utgångspunkt från ett undervisningstillfälle som dokumenteras så utvärderas och analyseras undervisningen och förändras med syfte att öka lärandet hos eleverna. Undervisningen genomförs med en helt ny grupp elever och cykeln som omfattar utveckling, dokumenterad undervisning, utveckling och undervisning för nya elever, genomförs ett antal gånger. Utifrån elevernas provresultat före och efter undervisningstillfällena kan forskarna dra slutsatser om undervisningens resultat.
– Ett exempel är hur elever i mellanstadiet hade problem med att avgöra hur de skulle kunna bestämma storleken på en vinkel. Det visade sig i ett forskningsprojekt, en learning study, att eleverna uppfattade uppgiften på ett annat sätt än vad lärarna förutsett. Lärarna och forskarna upptäckte i förtestet att eleverna exempelvis inte förstod att sidornas längd, vinkelbenen, inte hade någon betydelse för uppgiftens lösning.
– När lärarna identifierat att vinkelbenens längd tillskrevs betydelse hos ett flertal elever designade läraren uppgifter som skulle hjälp eleverna att urskilja de aspekter som bestämmer vinkelns storlek.
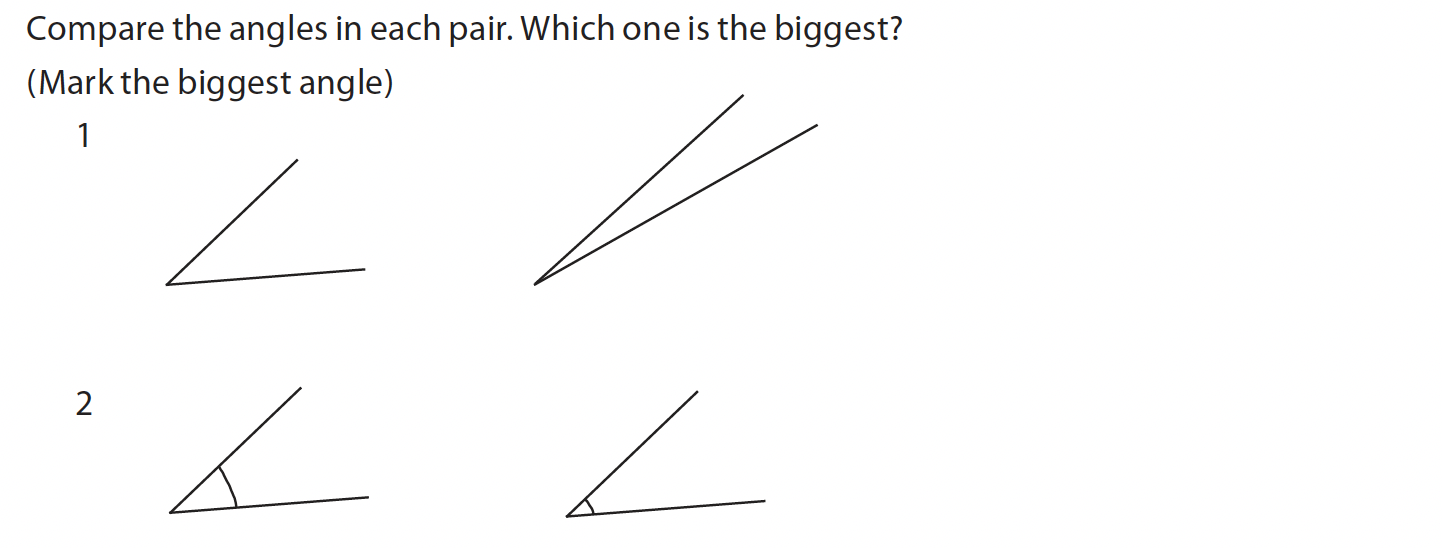
Ett forskningsprojekt som utvecklade undervisningen med en så kallad learning study, visade bland annat att olika långa vinkelben gav oförutsedda konsekvenser för lärandet om vinkelstorlek.
Behöver analysera felsvaren och frågorna
Grundläggande för att utveckla undervisningen i learning studies är variationsteori som går ut på att hitta vad som kan vara konstant och vad som kan varieras för att elever ska utveckla förståelse. I exemplet med vinkelmätning noterade lärarna att det var vinkelvridningen eleverna behövde hålla i fokus. Då urskiljde eleverna de aspekter som lärarna hade sett som centrala för begreppsförståelsen.
Inger Eriksson menar att forskare och lärare generellt känner till ganska väl vad eleverna har problem med, men inte lika väl varför.
– Som med vinkelbegreppet och mellanstadieeleverna. Lärarna hade inte räknat med att längden på vinkelbenen skulle ha någon betydelse, men fick reda på det tack vare att de genomförde ett förtest som de kunde ha som utgångspunkt för designa relevanta variationsmönster. Som lärare kanske man behöver analysera både elevernas felsvar och elevernas egna frågeställningar för att förstå vad de inte har förstått.
Både typiska nationella och lokala fel
Forskning visar att det finns fel som är typiska hos elever i hela Sverige, men också fel som är lokala och kan bero på en viss undervisning som är lärarberoende eller knuten till en viss skolas undervisning.
– För att utveckla undervisningen med uppgifter kan man som lärare analysera elevernas prov eller resultaten i matteböckernas uppgifter för att se om man hittar ett mönster.
”Fick inte rätt stöd”
Inger Erikssons intresse för lärande och undervisning väcktes redan när hon själv gick i skolan. Elever i hennes klass kom efter i undervisningen och fick inte chansen att lära.
– Då blev jag frustrerad för att jag uppfattade att de inte fick rätt stöd. I dag tänker jag snarare att undervisningen inte hade utvecklats i takt med utvecklingen av vad vi behöver klara av i samhället. Så har det varit länge och kan vara än idag: att undervisningen är anpassad för kraven som ställdes för länge sen. Tidigare var det viktigt att kunna huvudräkning, men hur viktigt är det idag om du exempelvis jobbar i en kassa eller i en butik? Inte så att huvudräkning inte kan vara bra för eleverna att lära sig men idag har huvudräkningen en annan funktion som att till exempel kunna göra överslag och bedöma rimlighet i svar.

Inger Eriksson har i flera forskningsprojekt om matematikundervising tillämpat forskarna Vasilii Davydov och Daniil Elkonins teorier om lärandeverksamhet.
Kritisk till uppmuntran av snabb problemlösning
Inger Eriksson har forskat i större delen av sitt yrkesliv inom pedagogik och didaktik, men har fokuserat på matematik de senaste 20 åren. Hon ser stora möjligheter till utveckling av undervisningen och är kritisk till en dominerande klassrumskultur som uppmuntrar att eleverna löser problemen snabbt och rätt i stället för att få chansen att resonera och ta tid på sig för att lösa komplexa och utvecklande uppgifter.
– I dag går undervisningen och läromedlen i matematik oftast från de enkla till de komplexa problemen. Men det innebär att många elever aldrig får möjlighet att jobba med de komplexa problemen: de hinner inte till uppgifterna där det principiella innehållet faktiskt finns, som ger förståelse. Att låta eleverna göra uppgifter som inte gör dem mer förtrogna med matematik är att svika dem på ett sätt.
”Även tidig undervisning kan omfatta komplexa problem”
Inger Eriksson lyfter fram marknadsföring och opinionspåverkan via sociala medier, baserad på algoritmer, som ett exempel på varför undervisningen bör leda till djupare förståelse och inte främst färdighet att räkna snabbt.
– Eleverna behöver förstå varför det kan vara problematiskt att beslut och marknadsföring är baserad på big data för att kunna förhålla sig kritiska till den typen av samhällsfenomen.
– Istället för att elever sitter och tragglar med sånt som de kan lära sig på köpet – när de jobbar med lite mera intressanta uppgifter – kan även den tidiga undervisningen omfatta de komplexa problemen. Vi är präglade av idén att barnen måste ha grunderna först, men vi behöver reflektera kring vad grunderna faktiskt består av. Vi vet från studier att komplexa uppgifter väcker elevernas nyfikenhet och att elever som kan föra och följa exempelvis algebraiska resonemang ofta lyckas bra även på andra områden i matematiken.
15 september 2025 | Text: Johan Boström | Foto: Oskar Omne
Referenser och lästips
- Eriksson, I., Adolfsson Boman, M., Jansson, A., Hverven, M., & Tambour, T. (2013). Att introducera likhetstecken i ett algebraiskt sammanhang för elever i årskurs 1. Forskning Om Undervisning Och lärande, 1(10), 29–49.
doi.org/10.61998/forskul.v1i10.27607 - Eriksson, H., & Eriksson, I. (2016). Matematik som teoretiskt arbete – utveckling av matematiska modeller för rationella tal i åk 4. Forskning Om Undervisning Och lärande, 4(1), 6–24.
doi.org/10.61998/forskul.v4i1.27502 - Wettergren, S., Eriksson, I., & Tambour, T. (2021). Yngre elevers uppfattningar av det matematiska i algebraiska uttryck. LUMAT: International Journal on Math, Science and Technology Education, 9(1), 1–28.
doi.org/10.31129/LUMAT.9.1.1377 - Eriksson, I., Fred, J., Nordin, A.-K., Nyman, M., & Wettergren, S. (2021). Tasks, tools, and mediated actions – promoting collective theoretical work on algebraic expressions. Nordic Studies in Mathematics Education (NOMAD), 26(3–4), 29–52
- Runesson, U. (2007). A collective enquiry into critical aspects of teaching the concept of angles. Nordic Studies in Mathematics Education (NOMAD),12(4) 7–25.
- Bentley, P-O., & Bentley, C. (2017). Mattemissar, orsaker och åtgärder – ett analysmaterial för 7-9. Liber.
liber.se/webshop/product/mattemissar-orsaker-och-atgarder-ett-analysmaterial-for-7-9-9789147116096





